随着计算机计算能力的不断提高,机器学习这一技术在各个工业领域中逐渐得到应用。与此同时,随着国内风电平价上网进程的推进,风电场后评估工作在风电行业内不断受到关注;而风电机组性能评估作为风电场后评估工作中最重要的内容之一,其与机器学习技术的结合自然受到了行业内的广泛关注[1-2]。
风电机组性能评估依赖于建立风电机组性能模型,即建立风电机组输出功率与风电机组各关键参数( 如风速、桨距角、偏航角等) 之间的函数关系,这属于典型的非线性回归问题;在机器学习领域,深度神经网络是解决该问题的经典手段,因此,利用其构建风电机组性能模型自然得到了行业内研究者的广泛尝试。比如,文献[3]尝试将神经网络拟合的风电机组功率曲线与测量的风电机组功率曲线进行对比分析;文献[4] 验证了采用卷积神经网络构建的风电机组齿轮箱故障识别分类器比一般的支持向量机(SVM) 分类器具备更好的性能表现;文献[5] 提出了基于引力搜索算法优化人工神经网络的风电机组传动链故障诊断方法;文献[6] 采用深度神经网络构建了风电机组齿轮箱状况检测框架,以用于故障预警;文献[7] 利用线性混合自组织映射神经网络对风力机状态特征进行分类,提出了一种特征变化累积趋势差分法,用于预测风力机的异常和故障。上述研究的关注点主要在于深度神经网络在具体场景中的实际应用,所构建的模型大多仅针对研究中所使用的特定风电机组。
综上,本文尝试从深度神经网络本身出发,探讨其自身超参数的取值对最终风电机组性能模型的准确度的影响,同时将验证以上超参数在参考风电机组训练中得到的最优配置是否可以直接推广应用于同一风电场同一型号的其他风电机组上。针对以上研究内容,本文首先介绍了深度神经网络的基本概念及所选取的超参数,并从某实际运行的风电场50 台2000 kW 风电机组中选取1 台作为参考风电机组,基于该机组的SCADA数据采用深度神经网络进行训练,通过网格搜索(Grid Search) 法得到最优的超参数配置方案,并验证该配置方案是否为整个风电场的全局最优配置。
1 深度神经网络的概念及超参数的选取
1.1 深度神经网络的概念
深度神经网络(Deep Neural Network,DNN)是具有多个隐含层的人工神经网络[8],其由3 部分构成,分别为输入层、隐含层及输出层。每一层都由一定数量的神经元构成,同时每个神经元都具有1 个自己的激活函数,当其接收到的信号达到激活函数的阈值时,其将被激活,并向下层连接的神经元输出信号,最终各层的神经元逐一连接在一起构成一个类似生物神经的网状结构。具有3 个隐含层的深度神经网络结构示意图如图1 所示。其中,Xi 为选定的进入深度神经网络输入层参与风电机组性能模型构建的、与风电机组输出功率相关性较高的SCADA 数据类型,如风速等;Y 为风电机组实际输出功率。
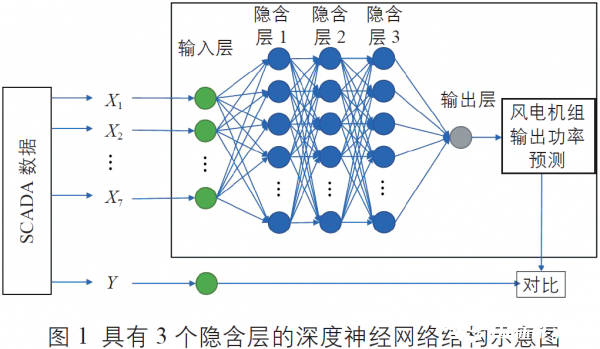
1.2 超参数的选取
深度神经网络的结构和特性是通过超参数来决定的,超参数是在深度神经网络训练过程开始之前需要设置数值的参数,而不是通过训练得到的参数数值。通常情况下,需要对超参数进行优化,以寻找到一组最优的超参数,提高训练效果。深度神经网络的超参数很多,包括但不局限于:
1) 隐含层的层数;
2) 深度神经网络的形状;
3) 每层隐含层神经元的数量;
4) 神经元的激活函数;
5) 损失函数;
6) 优化器的选择;
7) 隐含层传递权重初始化方法。
这些超参数对于深度神经网络的影响不尽相同,其中有些会影响最终的训练效果,有些会影响训练过程的速度和收敛。由于本研究仅针对风电机组性能模型构建中影响深度神经网络最终训练效果的超参数,因此基于参考风电机组的训练过程,选取深度神经网络隐含层层数、深度神经网络形状及隐含层神经元数量这3 个超参数作为主要研究对象,并寻找其最优配置方案[9]。
1.2.1 深度神经网络隐含层层数
深度神经网络模型中,输入层与输出层之间隐含层的层数决定了模型的复杂程度。一般情况下,隐含层的层数越多,模型的复杂程度就越高,也就越能更好地模拟复杂问题;但相应地,模型训练所需要的时间也会相应增大,并且可能会伴随出现“过拟合”的问题。针对本研究中风电机组发电性能的问题,输入层的神经元数量为7,输出层的神经元数量为1,属于机器学习中相对简单的案例,因此,所采用的隐含层层数不需要过多。
1.2.2 深度神经网络形状
当深度神经网络的隐含层层数确定后,每一层隐含层的神经元数量决定了深度神经网络的形状,实际应用中较为常见的形状为漏斗型和均衡型。
1.2.3 隐含层神经元数量
本研究中的隐含层神经元数量是指输入层之后的第一层隐含层的神经元数量。对于漏斗型深度神经网络形状来说,输入层之后的每一层隐含层的神经元数量与前一层相比,均按一定比例递减( 本研究中采用0.5 倍递减);对于均衡型深度神经网络形状而言,输入层之后的每一层隐含层神经元数量均与第一层相同。图1 所示的即为1个典型的均衡型3 层隐含层深度神经网络形状。与深度神经网络的层数类似,每一层隐含层的神经元数量越多,表明该模型越复杂,增加隐含层神经元数量可以更好地模拟复杂问题,但机器学习的时间成本也相应更高,并且随着神经元数量的增长,也会出现“过拟合”问题。
2 超参数寻优
本研究选取了某个实际运行的风电场进行方案验证。该风电场的装机容量为100 MW,由50 台2000 kW 风电机组构成,风电机组采用SCADA 系统,共可采集90 种数据类型,采用10 min 时间步长,共记录了9 个月的数据。
本研究采用基于互信息的关键数据提取方法[10],从中选取了7 个与风电机组输出功率“相关性”较高的数据类型作为深度神经网络训练输入层的入口数据。这7 个数据类型的名称及对应单位如表1 所示。

首先选取了编号为T1 的风电机组作为参考风电机组进行训练,然后以训练后模型预测的风电机组输出功率PDNN 与SCADA 数据中实际记录的风电机组输出功率PSCADA 间的均方误差MSE 作为损失函数来进行深度神经网络3 个超参数的寻优。均方误差MSE 的计算公式为:
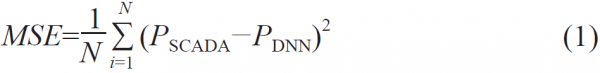
针对深度神经网络隐含层层数、深度神经网络形状及隐含层神经元数量这3 个超参数,本研究设置的可选配置如表2 所示。

对于前文提到的其他超参数,本研究中则采用了机器学习领域中的经典配置,具体的配置方案如表3 所示。本研究通过Grid Search 的方法对超参数进行寻优,即将3 个超参数所有配置排列组合后的全部方案均进行模型训练,最终选取结果最优的方案。每个不同超参数组合配置的训练采用2000 批次(epoch),每批次300 批大小(batchsize),最终参考风电机组T1 在不同超参数配置下的风电机组性能模型训练效果如表4 所示。

从表4 的训练结果可以看出,在参考风电机组T1 上,最优的超参数配置为:隐含层层数取5、深度神经网络形状为漏斗型、隐含层神经元数量为64;该配置下达到的测试数据集误差为6.95kW,相对于风电机组的额定功率2000 kW 而言,该值所占比例仅为0.35%。而表现最差的配置方案为:隐含层层数取4、深度神经网络形状为均衡型、隐含层神经元数量为256;该配置下达到的测试数据集误差为16.77 kW,相对于风电机组的额定功率2000 kW 而言,该值所占比例为0.84%。由此可以得到以下结论:
1) 在不同的超参数配置方案下,通过深度神经网络训练得到的各个风电机组性能模型应用于参考风电机组后的预测准确度之间存在一定差异。
2) 从工业角度来看,在不同的超参数配置方案下,深度神经网络训练得到的风电机组性能模型应用于参考风电机组后的准确度误差基本可以忽略不计。因此,若只是针对参考风电机组进行模型构建,可以直接将超参数选择为训练速度最快的配置方案,即隐含层层数最少、神经元数量最小。
下文对表2、表3 中的超参数设置在参考风电机组上的最优配置与同一风电场中同一型号其他所有风电机组上的最优配置间的相对关系进行探讨。理想情况下希望实现以下2点假设:
1) 参考风电机组的最优配置同时也是同一风电场中同一型号其他风电机组的最优配置;
2) 基于参考风电机组得到的性能模型,应用于同一风电场同一型号其他所有风电机组上时准确度也能满足需求。假设1) 和假设2) 若能同时被验证成功,则说明同一个风电场中同一型号风电机组的最优超参数的配置及基于参考风电机组得到的性能模型具有推广性。这也意味着在实际应用中,不需要针对每台风电机组单独进行训练,只需要选择1台参考风电机组进行训练,再推广到整个风电场即可,从而可大幅节省时间,更能满足工业领域的需求。
为了进行以上2 个假设的验证,本研究将参考风电机组T1 训练得到的不同超参数配置下的深度神经网络模型分别在风电机组T2~T50 上进行复用,以在风电机组T2~T50 上模型的预测输出功率与实际输出功率的均方误差的平均值作为评价标准,结果如表5 所示。
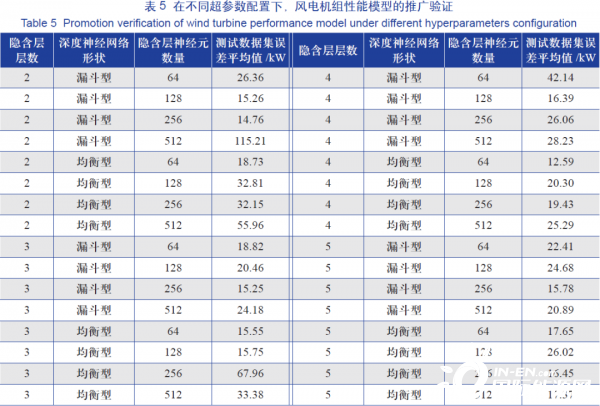
通过分析T2~T50 这49 台风电机组应用参考风电机组T1 经深度神经网络训练得到的模型后的最终结果可以发现:
1) 在参考风电机组T1 上验证的最优超参数配置方案,在T2~T50 风电机组上的表现并非最优。
2) 在T2~T50 风电机组上表现最优的超参数配置方案( 隐含层层数为4、深度神经网络形状为均衡型、隐含层神经元数量为64),在参考风电机组T1 上的表现也较好。
3) 基于不同超参数配置的深度神经网络训练得到的模型,训练结果在风电机组T2~T50 上的表现总体较好,各模型的平均的均方误差平均值为27.32 kW,最优的均方误差平均值为12.59kW,最不理想的均方误差平均值为115.21 kW,相对于风电机组的额定功率2000 kW 而言,均方误差平均值占比分别为1.37%、0.63% 和5.76%。综上所述,虽然前文中的假设并未完全得到验证,但由于基于参考风电机组得到的性能排名靠前的超参数配置方案应用于本风电场中同一型号其他风电机组时,虽然性能不是最优但基本也较为靠前,同时准确度也在可接受范围内,因此,在工业应用中基本可以认为该方式具备推广性。即实际应用中,出于时间成本考虑,可以将基于参考风电机组得到的超参数配置方案及模型直接应用于本风电场中同型号的其他风电机组。
3 结论与建议
本文以某实际运行风电场的50 台2000 kW风电机组的SCADA 数据为基础,对采用深度神经网络技术建立风电机组性能模型时的隐含层层数、深度神经网络形状及隐含层神经元数量这3个超参数的取值对于该模型构建效果的影响进行了分析。通过Grid Search 方法在参考风电机组上发现这3 个超参数配置不同时建立的模型的最终性能存在一定差异,但从工业应用角度考虑,差异基本可以忽略不计。同时分析还发现,参考风电机组采用最优超参数配置方案时训练得到的模型应用于同一风电场中同一型号的其他风电机组时得到的并非最佳方案,但由于其在同一风电场中同一型号的其他风电机组上的预测准确度在所有配置方案中仍然较优,因此出于时间成本考虑,在工业应用中可以认为同一风电场中同型号的风电机组间可以应用此方案,采用深度神经网络在参考风电机组上得到的最优模型具备推广性。
基于本研究的方法与结论,在未来工作中可以进一步针对不同型号的风电机组或不同风电场的风电机组进行超参数配置方案的寻优及推广性验证。若基于参考风电机组训练得到的风电机组性能模型在不同机型乃至不同风电场间可以直接推广复用,则可进一步为机器学习技术在风电行业后评估工作中的应用确立更为普遍的事实依据。
 中国能源资讯网
中国能源资讯网


