浮式海上风电 (Floating offshore wind, FOW) 对于欧洲的能源目标的实现至关重要。然而,系泊系统的材料和安装成本很高,降低成本迫在眉睫。因此开发商正在积极探索适用于浮式风电场的新型系泊概念。
一项创新的建议是,在传统的悬挂在浮体和海床之间的锚索的基础上,引入两个浮体之间的共享系泊系统。
模拟具有共享系泊的风电场 – 以及对更快速的分析方法的需求
共享系泊系统的引入使得模拟和分析中需要包含更多的机械耦合因素。共享系泊系统目前是 SFI BLUES 和 CYBERLAB KPN的联合研究课题,得到了挪威研究委员会和工业界合作伙伴的资助。
能够处理互连浮体系统的高精度模拟软件,有 OrcaFlex 和 Sima,后者由 SINTEF Ocean 开发。这些工具通常基于非线性有限元方法 (Finite element method, FEM),其缺点是计算量大,需要数小时甚至数天才能完成在最大位移、张力极值和疲劳寿命方面的必要计算。这显然无法满足设计工程师在大量设计方案和载况情况下寻找最佳设计的快速计算需求。设计工作中既需要简化(且快速)的方法,也需要高精度(且较慢)的方法。对于单个浮体来说是如此,对于浮式风机的耦合系统来说更是如此。
为了在不牺牲太多准确性的前提下提高分析速度,研究人员正在开发简化的方法。这些简化方法就是仅关注当前问题中重要的物理效应,同时忽略不重要的物理效应。Sima(Simo求解器)、Mimosa 和 OrcaFlex 中都有的一种广泛使用的简化系泊缆分析,采用准静态模型,忽略阻尼和惯性引起的动态效应。在某些情况下,根据模型试验或更复杂模型,并基于一定的经验添加缺失的阻尼来“修复”后,该模型能取得令人满意的结果。但在其他情况下,如果存在更强的动态系泊缆效应的情况下,准静态结果是完全错误的。对于这些情况,我们需要重新考虑之前的假设,并加入缺失的物理效应。
另一种简化是基于线性化。线性化模型,无论是准静态还是全动态,都可以在频域中进行分析,速度特别快。然而,极端海况下的系泊浮体通常会表现出超出系泊缆线性响应范围的大幅低频运动(缓慢漂移)。此外,频域工具必须分别分析波频 (Wave-frequency, WF) 和低频 (Low-frequency, LF) 响应,尽管我们知道 WF 和 LF 响应分量之间存在强烈的非线性相互作用。虽然频域方法肯定有其用武之地,但我们仍需要更准确且快速的方法。
一种快速模拟系泊缆动力学的新方法
出于对更快速方法的渴求,以及对现有简化方法的缺点和不准确性的认识,作为 SFI Blues 项目的一部分,研究人员开发了一种新的简化系泊缆模型。在深入研究新方法的内部工作原理之前,最重要的问题是:它有效吗?
我们最近在半潜型浮式风机 WINDMOOR 上测试了该方法,它是 WINDMOOR KPN 项目开发的一部分,并作为 Sima 软件包中的示例模型。WINDMOOR浮体有3条相同的系泊缆,每条系泊缆均配有25米长的顶部锚链、170米长的纤维缆和400米长的躺底锚链,作业水深150米。首先,我们针对极端海况,运行Sima对Simo-Riflex 耦合模型进行模拟,以获得浮体运动和系泊缆张力。然后,利用 Simo-Riflex模型的浮体运动数据来规定新方法中导缆器的运动。同时,在传统的准静态模型上进行同样的分析以进行比较。下图为三种方法得出的三条系泊缆的张力时间序列的比较。
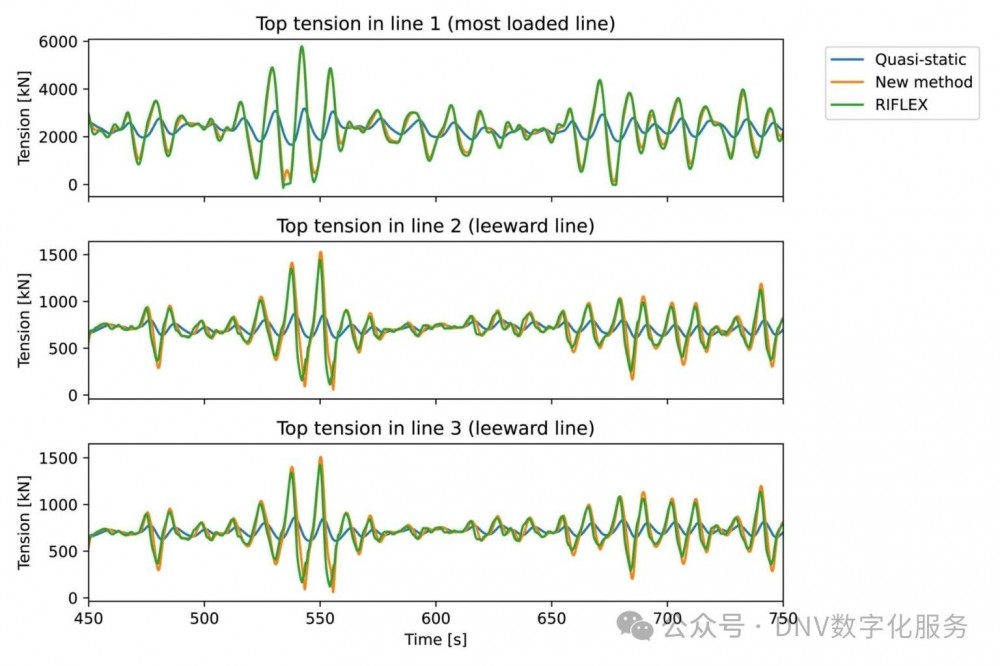
我们发现准静态模型在这种情况下完全失效,而新方法给出了与非线性有限元 (Simo-Riflex) 非常接近的结果。准静态模型除了对张力的普遍低估之外,还可以发现有明显的相位差。新方法和有限元法预测的张力峰值早于准静态模型预测的峰值。这是因为阻力载荷,它产生与浮体速度同相的力——阻尼力。这些阻尼力对于浮体的低频运动非常重要,这一事实表明,新方法非常适用于运动预测。这也意味着对选定的系泊缆进行基于导缆器运动的非线性有限元分析,可以用来验证或改进张力预测,即所谓的非耦合系泊分析。
尽管新方法的开发始于共享系泊的风场,但软件应用的最初场景仅限于系泊缆的计算。我们将进一步推广这一新方法,以支持共享系泊缆的分析,并将其应用于更多的新型系统和条件下,以确定其有效范围。它在更深的水中也同样有效吗?用于带有配重块和浮标的系统怎么样?一旦经过彻底验证,我们将通过Sima软件包将新模型提供给业界使用。现在,这种新方法已成为新开发的软件库 fmoor 的一部分。

这一切是如何运作的(技术详解!)
让我们一起深入探讨这一新方法的内部工作原理,新方法的灵感来自于所谓的简化分析法(Simplified analytic method, SAM),这一概念通常在频域系泊分析工具 Mimosa 中得以应用。然而,SAM的一个显著局限性在于其是线性的,我们的新方法则彻底摒弃了这一限制,实现了完全的非线性处理。新方法的推导基于18世纪后逐渐发展起来的分析力学中的能量法。与牛顿力学——由艾萨克·牛顿一个世纪前所创立,并主要关注运动矢量——不同,分析力学通过广义牛顿运动方程允许我们自由选择坐标,即广义坐标。这一灵活性为我们的新方法提供了坚实的数学基础。分析力学是结构力学中模态分析的基础,其中结构的变形被描述为预定义的模态振型的加权和。模态分析通常针对线性结构模型进行,模态振型通常被视为结构的本征模态。线性假设和选择本征模态作为模态振型给出了特别简单且解耦的运动方程。但无论是线性还是选择本征模态作为模态振型都不是分析力学的必要条件,而且我们的新系泊缆模型确实是完全非线性的。
在分析力学框架下,制定非线性运动方程,涉及到两个关键的标量能量函数:1) 作为广义坐标函数的总势能,以及 2) 作为广义坐标函数的总动能及其时间导数。与势能相关的力主要源自重力、浮力和弹性应变,这些代表刚度或回复力。与动能相关的力则是由系泊缆的质量和附加质量而产生的惯性力。为了平衡这些内部力,我们还需要考虑外部载荷,如系泊缆两端(来自海床和浮体)的受力,以及水动力阻力(包括阻尼和激励)沿系泊缆产生的载荷。这些外部载荷的大小和性质对于确保非线性运动方程的准确性至关重要。广义外部载荷的大小是沿系泊缆载荷分布以及载荷模式与给定振型的匹配程度的乘积。
至此,我们提出一个重要的假设:只需将动能设置为零,就可以忽略惯性效应。通过查看系泊缆横截面在流场中的Keulegan–Carpenter (KC) 数,可支持这一假设。KC数是运动幅度与系泊缆直径的比值。高KC值意味着粘性流效应相对于惯性效应更加重要,对于系泊缆来说确实如此。
那么如何选择振型呢?这些必须反映模型中包含的物理效应。当仅包括势能效应(重力、浮力和材料应变/应力)时,我们知道系泊缆将呈现静态悬链线形状,遵循弹性悬链线方程。因此,悬链线形状似乎是一个很好的起点。但我们还有一个额外的物理效应:沿系泊缆的粘性阻力。因此,我们必须对悬链线形状进行小扰动。这种扰动允许系泊缆随拖曳力产生轴向伸长。振型中的这种额外变形还必须伴随势能函数中的附加项,以获得正确的力。虽然伸长率对于位移来说非常小,但当对时间进行微分以获得速度时,伸长率会变得更大。事实上,通过滤除沿系泊缆法向速度的高频成分,这种小的附加伸长在“调节”阻力载荷方面发挥着重要作用。试图采用未经修改的悬链线方程并包括拖曳力载荷是根本行不通的——因为系泊缆的法向速度和拖曳力载荷将被严重高估。额外的伸长解决了这个问题,并允许我们的模型捕捉文献中称为“拖曳锁定”的物理现象。当导缆器一端的高频振荡激发系泊缆上非常大的法向拖曳力载荷时,会发生拖曳锁定,此时系泊缆在横向上(变形,编者注)几乎完全受限,仅允许弹性和轴向变形。
能量法与传统有限元方法
能量法的优点在于运动坐标和相关振型的任意性。如果能够做出正确的选择,再结合需要解决的的问题,我们只需几个坐标就可以解决问题。我们的模型仅使用三个坐标来描述系泊缆的响应。这比有限元方法中所需的坐标数量小一两个数量级,后者沿系泊缆的每个节点都有 3 个坐标。换句话说,我们需要解的方程少得多。我们的方程也比来自有限元方法的方程“更友好”——是因为它们不包括刚性/快速动力学。快速动力学通常没有什么物理意义,但仍然需要通过使用过小的时间步长来解决,并且经常会造成严重(数值,编者注)挑战(使模拟崩溃!)
能量法的一个潜在缺点是,用数学方法写出能量函数是一件令人头疼的事,更糟糕的是,要计算能量函数相对于所有广义坐标的导数。在我们的例子中,写出势能是可行的。在计算导数时,我们利用一种令人着迷的计算技术——通过运算符重载的前向模式自动微分,在下文中称为自动微分。自动微分是一种提供精确导数的方法,无需将解析结果写为源代码。
我们坚信,分析力学的能量法与能量函数的自动微分相结合,为我们开发快速且准确的新方法提供了所需的基础。系泊系统模型的改变,包括惯性效应,以及添加了新的模态振型,可允许更丰富的响应模式,这也是未来发展的可能路径。
 中国能源资讯网
中国能源资讯网


