风电机组叶片流固耦合的数值模拟方法

随着风电机组单机容量的不断增大，风电机组叶片尺寸也越来越长。对于超长风电机组叶片的气动计算及结构计算，常规的叶片刚性体假设所引起的误差越来越大，因此必须考虑叶片在风载条件下结构变形对气动力的影响。流固耦合(fluid-structure interaction, FSI)是研究风电机组叶片气弹特性及结构特性的重要手段，国内外通过流固耦合对叶片的结构响应、流场变化、叶片载荷分布等特性进行了一系列研究。流固耦合按照求解方法可分为完全耦合和交替求解。李媛等以MPCCI为数据交换平台连接商用CFD,CSD软件，模拟考虑风切变时轮毂高度额定风速下的风轮全三维流固耦合，分析了风剪切对叶片绕流、变形以及耦合作用对载荷分布的影响规律。胡丹梅等采用k-SST紊流模型和滑移网格技术，对海上风电机组叶片进行了流固藕合计算分析，发现叶片流固耦合作用使叶片气动攻角、扭矩增大。Zahle等采用不可压缩重叠网格技术，分析了水平轴风电机组风轮与塔架间的耦合作用。Hsu等通过对5 MW三叶片水平轴风电机组风轮在有无塔架情况下进行了流固耦合研究，发现叶片转过塔架时由于塔影效应使单个叶片气动扭矩降低10%-12%。 Zhang等通过对比研究，发现风切变对风电机组叶片变形及应力的影响明显大于流固耦合所产生的作用。任年鑫等基于三维黏性不可压缩Navier-Stokes方程和重整化群k-ε(RNG)湍流模型，数值模拟美国可再生能源实验室(NREL)5 MW海上风电机组的气动性能，并研究了浮式平台不同运动幅值及运动周期对风电机组叶片气动性能的影响规律。陈海萍等选用k-ε湍流模型，将风作为黏性不卡压缩流体，计算出流固耦合作用下风电机组叶片的应变分布。李德源等采用计算多体系统动力学理论，基于R-W(Roberson-Wittenburg)建模方法，建立柔性叶片的气弹耦合方程，结合相应的风电机组气动载荷分析模块，实现了叶片的气弹耦合分析。王旭东等将叶片的启动与结构力学模型进行耦合，研究叶片变形对来流的影响，提出一种旋转叶片结构性能分析方法。Dong等应用CFD-CSD祸合方法对风电机组叶片的载荷及气弹特性进行研究，发现叶片气弹变形显著降低气动载荷。MEXICO (model experiment incontrolled conditions)实验是由欧盟资助的一项大型风电机组实验。梁明轩通过对叶片模态分析得到叶片各阶模态，发现叶片扭转、挥舞、摆振三者之间的耦合，并对叶片气动弹性问题进行研究，建立叶片颤振方程，确定了叶片颤振发散条件。杨华等应用风电机组旋转叶片表面压力的三维PIV(particle image velocimetry)流场测量方法，测试得到无偏航工况下叶片上5个测试断面的表面压力系数分布，并计算了该工况下叶轮所受的轴向力和切向力。潘旭运用Ansys、CFX基于Ansys Workbench软件平台对某MW级水平轴风电机组叶片进行流固耦合数值模拟，分析了藕合过程中叶片的变形及应力变化。陆洋等利用Newmark数值积分法获得叶片气弹响应的稳态周期解，分别以NREL Phase VI非定常空气动力学实验及其公开的1.5 MW风电机组叶片为算例计算了有/无预弯叶片的气弹响应。以上研究均通过建立风轮旋转的计算模型对风轮流固祸合进行研究，网格划分困难，涉及到移动域与静止域网格匹配等复杂过程，计算成本高。为此，本文采用风切变形式模拟风轮旋转及来流风速的综合效应，研究风电机组叶片流固耦合数值模拟的一种新方法。

1流体计算模型

1.1流体域求解方法

流场中的控制体既不能产生质量也不能消灭质量，因此它满足质量守恒定律。该定律在流场中的数学表达式为连续性方程

式中，p,t,V分别为流体密度、时间和流体速度。

动量守恒定律可表述为：控制体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。其在流场中的数学表达式为运动方程

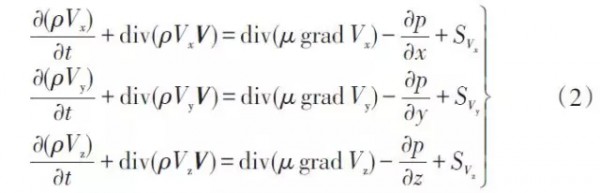
能量守恒定律是流动系统必须满足的基本定理，在不考虑温度变化条件下，其数学表达式为

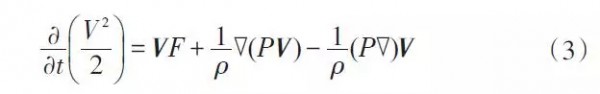
式中，F为质量力，P 为表面压强。

1.2叶素速度

风电机组风轮运行过程中实际参考风速为来流风速和旋转风速的共同作用，通过改变叶片不同叶展处的风速可实现正常来流风速和旋转风速的叠加效果。不同叶展处的参考风速Vref的计算公式为

式中，Vo为自然来流风速;w 为风轮旋转角速度;r 为叶展位置的旋转半径;a为轴向诱导系数;a’为切向诱导系数。

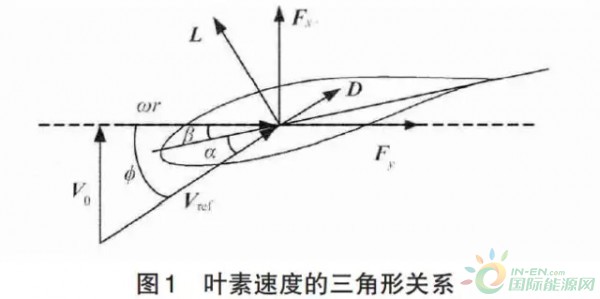
叶素速度矢量的三角形关系如图1所示，图中α、β、Ø分

2结构计算模型

2.1结构计算方法

风电机组叶片为多自由度有阻尼的非线性结构，其结构动力学运动方程为

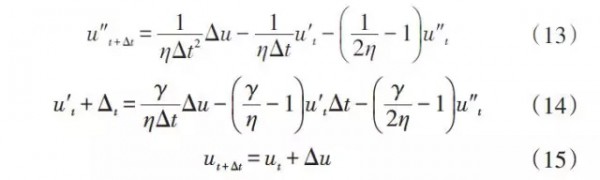
2.2叶片结构模型

为了用静止叶片模拟叶片旋转效应，只通过将叶素处的速度按照速度矢量关系修正还不能达到应有效果，需要对叶片不同截面处翼型的气动扭角进行修正。如图1所示，以旋转导致的风速方向作为参考方向，将该截面处的翼型进行顺时针旋转，旋转角θ等于人流角Ø。新翼型各点坐标相对于原坐标的计算公式为

3边界条件

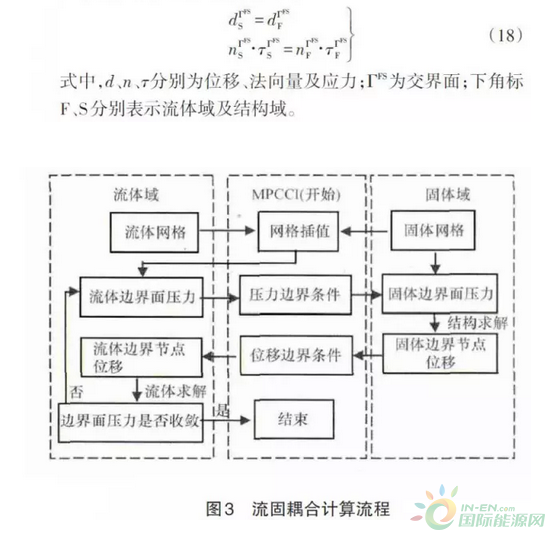
耦合系统以MPCCI为数据交换平台，采用弱耦合方式，数据传递过程中固体与流体分别求解，只在祸合界面上进行数据交换，祸合过程如图3所示。流固藕合交界面上分别满足边界位移及应力的连续性，即

4算例分析

4.1模型基本参数

以某年平均风速8 m/s 的二类风电场中5 MW风电机组叶片为研究对象，该机组风轮直径127 m，叶片长62 m，额定风速12.2 m/s，风轮额定转速13.5 r/min。在额定风速及额定转速条件下，根据上述方法对叶片进行计算，得到各翼展处的参考风速及修正角度如表1所示。

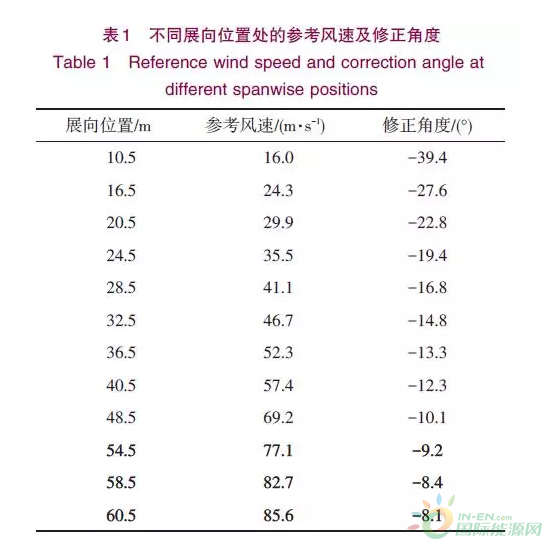
根据表1的参考风速及修正角度，进行风电机组叶片结构建模，得到修正前后叶片的结构模型(图2)。对修正后的结构模型进行有限元离散化，得到流场计算的全局网格及局部网格单元如图4所示。计算节点共计30万，网格单元共计86万。

采用等效质量、刚度分布的方法建立风电机组叶片壳结构模型。叶根段厚度为0.12 m，叶尖段为0.012 m，中间各段厚度沿展向线性变化，网格采用三角形壳单元S3R。节点总数5000，单元总数10000。用于结构计算的叶片有限元网格单元如图5所示。

4.2结果分析

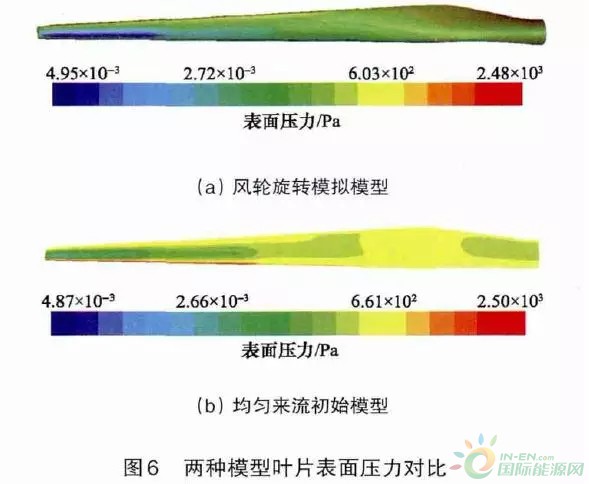
风轮旋转模拟模型与均匀来流初始模型的风电机组叶片表面压力计算结果对比如图6所示。两种模型的叶片表面压力呈现相同的变化规律，由叶根到叶尖逐渐减小;靠近叶尖处同一翼型截面上压力沿前缘到尾缘先迅速减小到最小值，后逐渐增大。数值上，旋转模拟模型叶片的表面压力小于均匀来流初始模型，整体误差小于5%,验证了风轮旋转模拟模型的可靠性。

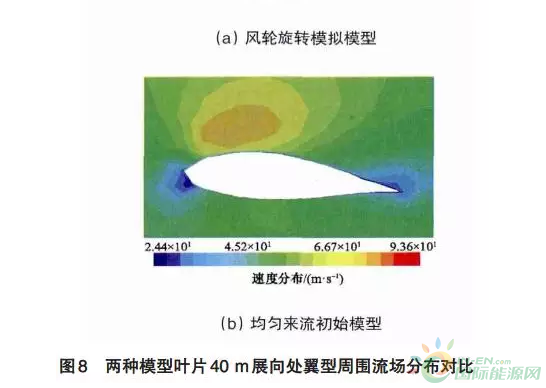
风轮旋转模拟模型与均匀来流初始模型的风电机组叶片40 m展向位置翼型周围气压、流速的计算结果如图7及图8所示

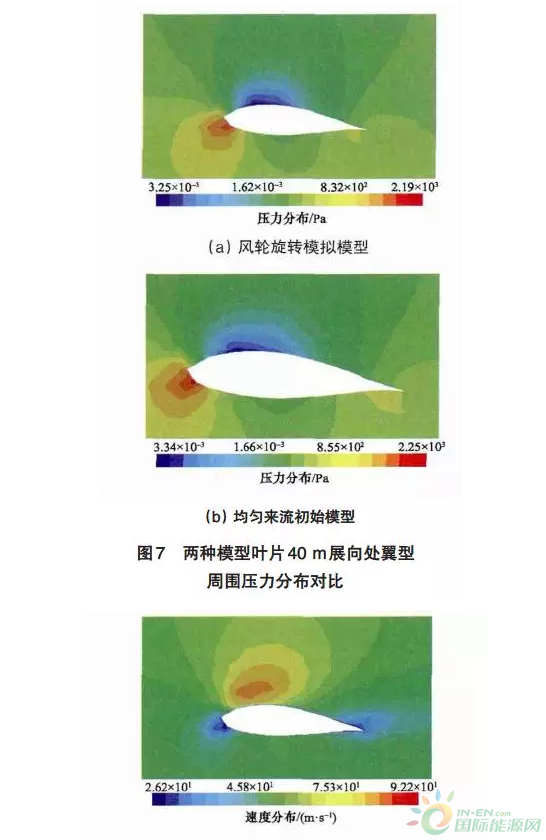
两种模型叶片40 m展向位置翼型周围气压分布，与MEXICO实验60%半径位置测试压力数据呈现相同的变化规律，翼型升力侧压力小于压力侧压力;翼型压力侧表面压力从前缘到尾缘呈现先减小后增大的变化趋势，最大压力位于前缘点靠下位置，最小压力位于升力侧30%弦长处。

两种模型叶片40 m展向位置翼型周围空气流速分布规律相同，翼型升力侧流速大于压力侧流速;翼型压力侧附近流速从前缘到尾缘先增大后减小，最小流速位于前缘点靠下位置，最大流速位于升力侧约25%弦长处。

两种模型叶片40 m展向位置翼型周围气压及流速计算结果的整体误差在3%以内。

风轮旋转模拟模型与均匀来流初始模型的风电机组叶片结构位移计算结果对比如图9所示。两种模型叶片的结构位移从叶根到叶尖逐渐增大，在叶尖达到最大值。旋转模拟模型叶片的最大结构位移计算结果为5.98 m，均匀来流初始模型叶片的最大结构位移计算结果为5.74 m，误差小于3%。

结论

以风切变形式模拟风轮旋转与来流风速综合效应，对风电机组叶片各展向位置翼型的扭角进行修正，提出一种用于风电机组叶片流固祸合数值模拟的风轮旋转模拟模型。在轮毂中心处风速为额定风速条件下，应用风轮旋转模拟模型对风电机组叶片进行三维流固耦合数值计算，并与均匀来流初始模型计算结果及文献实验结果进行了对比分析。风轮旋转模拟模型叶片40 m展向位置翼型周围气压的仿真计算结果与MEXICO实验测试结果的分布规律相同。两种模型叶片的表面压力、翼型周围气压及流速计算结果的分布规律相同，风轮旋转模拟模型得到的叶片面压力小于均匀来流初始模型的计算结果，整体误差小于5%;叶片40 m展向位置翼型周围气压及流速计算结果，以及叶片最大结构位移计算结果的误差均小于3%。